He preferido que esta quinta entrega cerrara el título «Experimentos, reflexiones y otros artefactos», y despedir estos mini artículos o mini serie, si es que se pueden llamar así, con un ejemplo un tanto más avanzado, pero en la linea de los anteriores. Así que me habeis tenido aperreado toda la semana, dándole vueltas a la cabeza sobre cómo iba a finalizar estas entradas. 🙂
No. No creais que es sencillo elegir el «experimento» ya que debe cumplir a priori algunas condiciones en cuanto a la extensión, a su complejidad, al uso de componentes que puedan ser compatibles en varias versiones y casi siempre en cuanto a que sea verdaderamente didáctico. Por lo que no vale cualquier idea que te venga a la cabeza, sino que tienes que pelearte con ella y ver si realmente te vale. Y os confieso cuando uno llega a casa tras la jornada diaria quedan pocas ganas de pelearse con nada (os pasará tambien a vosotros casi con seguridad). 🙂
En fin… Yo creo que sí que vale la pena el esfuerzo, y creo muchos de vosotros lo agradecereis.
¿Teneis ganas de trabajar un rato?
Venga, vamos allá.
Este era el ejemplo que se me ocurrió: Imaginaba que pudieramos tener la necesidad de calcular el modo más óptimo de recorrer una cantidad de puntos indefinido, eso sí, recorriendolos todos, desde un origen cualquiera hasta un destino cualquiera. Esa era la primera idea que me me vino a la mente. La idea además era vistosa, porque podíamos dibujar los puntos y las lineas sobre el formulario, lo cual no era demasiado difícil. Además, nos permitía seguir abordando el uso de clases muy básicas como las listas de punteros (TList), que muchos compañeros que dan sus primeros pasos pudieran no estar demasiado familiarizados.
El problema es que tras esa idea, existe una complejidad inherente que puede ser tan grande como uno quiera, por lo que decidí intentar abordarlo de una forma sencilla, aun a pesar de que pueda no ser optima. Y el criterio que se sigue para ordenar el camino que nos conduce desde el nodo (rojo) hasta el nodo (azul) sigue una pauta que se rige en calcular la menor distancia con respecto al nodo anterior, una vez ordenado el vector.
De hecho, si os fijais he puesto lineas mas arriba «¿Teneis ganas de trabajar un rato?» y lo he hecho porque os dejo para vosotros si quereis adaptarlo para que no considere todos los nodos sino el camino mínimo (fijado previamente una numero de puntos por los que haya que pasar) y no considere en la ruta todos, sino esa cantidad.
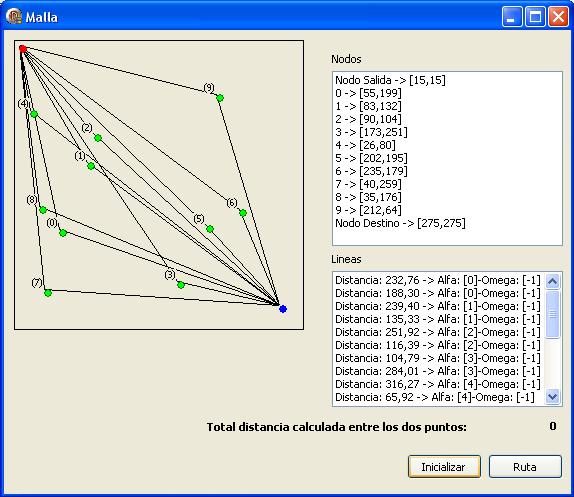
Al crearse el formulario, recrea una cantidad de nodos (he puesto 10 por poner una cifra) en puntos aleaotorios de un recuadro del formulario. El punto rojo es la salida (es otro nodo pero no es del vector). El punto azul el destino(tambien otro nodo que no existe en el vector). Ambos puntos, se enlazan a cada uno de los nodos del vector simplemente para que se pudiera ver una idea que voy a comentar posteriormente (*).
Esta es un imagen del formulario:
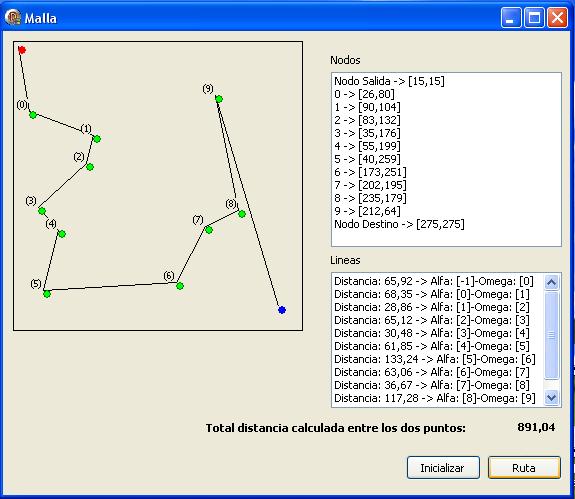
Asi que, como comentaba en lineas anteriores, vamos a recorrer el vector de nodos y reordenarlo sucesivamente hasta que se cumpla la precondición, que es que la ruta quede ordenada en función de la distacia al nodo que nos sirve de pivote, que va recorriendo la ruta que parte desde el punto de origen. Iniciamos en el punto de salida y buscamos el nodo mas cercano. Luego el más cercano a este. Y asi sucesivamente hasta llegar al punto de destino. En la imagen que figura tras el código se puede apreciar bastante bien.
Vamos a ver el módulo que hemos escrito para expresar esta idea:
unit UNodo;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls, Math;
type
TNodo = class;
TLinea = class;
TOrdenacion = procedure(Sender: TObject; ANodo:TNodo) of Object;
TMalla = Class(TObject)
private
FPivote: TNodo;
FLineas: TList;
FNodos: TList;
FZona: TForm;
FSalida: TNodo;
FDestino: TNodo;
procedure SetSalida(const Value: TNodo);
function GetLineas(Indice: Integer): TLinea;
function GetNodos(Indice: Integer): TNodo;
procedure InternalOrdenaNodos(Sender: TObject; ANodo: TNodo);
procedure VaciarLineas;
procedure VaciarNodos;
procedure DibujaRuta;
function CalculaMetricaRuta: Double;
protected
procedure DoOrdenaNodos(ANodo: TNodo; AOrdenacion: TOrdenacion); virtual;
procedure DoDibujarMalla; virtual;
procedure OrdenarNodos(ANodo: TNodo; ADestino: TNodo);overload; virtual;
public
FCambios: TStrings;
Constructor Create(AForm: TForm); virtual;
Destructor Destroy; override;
procedure InicializarMalla;
procedure OrdenarNodos; overload;
Function CountLineas: Integer;
Function CountNodos: Integer;
procedure ActualizarMalla;
function AddNodo: Integer;
function AddLinea: Integer;
function GenerarRuta: Double;
property Salida : TNodo read FSalida;
property Destino: TNodo read FDestino;
property Lineas[Indice: Integer]: TLinea read GetLineas;
property Nodos[Indice: Integer]: TNodo read GetNodos;
End;
TLinea = Class(TObject)
private
FMalla: TMalla;
FAlfa: TNodo;
FOmega: TNodo;
FDistancia: Double;
FIndice: Integer;
procedure SetAlfa(const Value: TNodo);
procedure SetOmega(const Value: TNodo);
procedure SetIndice(const Value: Integer);
protected
public
function GetDistancia: Double;
Constructor Create(AMalla: TMalla); virtual;
Destructor Destroy; override;
procedure Enlaza(AAlfa,AOmega: TNodo); overload;
procedure DibujarLinea;
property Alfa: TNodo read FAlfa write SetAlfa;
property Omega: TNodo read FOmega write SetOmega;
property Indice: Integer read FIndice write SetIndice;
End;
TNodo = Class(TObject)
private
FMalla: TMalla;
FShape: TShape;
FPoint: TPoint;
FPeso: Integer;
FTag: Integer;
function GetX: Integer;
procedure SetX(const Value: Integer);
function GetY: Integer;
procedure SetY(const Value: Integer);
procedure SetPeso(const Value: Integer);
procedure SetTag(const Value: Integer);
protected
public
function GetDistancia: Double;
function GetIndice: Integer;
function AddLinea(ANodoTarget: TNodo): Integer;
Constructor Create(AMalla: TMalla); virtual;
Destructor Destroy; override;
procedure DibujarNodo;
property X: Integer read GetX write SetX;
property Y: Integer read GetY write SetY;
property Peso: Integer read FPeso write SetPeso;
property Distancia: Double read GetDistancia;
property Tag: Integer read FTag write SetTag;
End;
implementation
function CalcularDistanciaNodos(AAlfa, AOmega: TNodo): Double;
//Necesitamos dos puntos (x1,y1) (x2,y2)
// [x1,y1] [x2,y2]
// Formula Raiz de ( ((x2-x1) al cuadrado) + ((y2-y1) al cuadrado) )
function CalcularDistancia(X1, Y1, X2, Y2: Integer): Double;
begin
Result:= SQrt(Power((X2-X1), 2) + Power((Y2-Y1), 2));
end;
begin
if (AAlfa = Nil) or (AOmega = Nil) then Result:= 0
else Result:= CalcularDistancia(AAlfa.X, AAlfa.Y, AOmega.X, AOmega.Y);
end;
{ TMalla }
procedure TMalla.ActualizarMalla;
begin
DoDibujarMalla;
end;
function TMalla.AddLinea: Integer;
begin
Result:= FLineas.Add(TLinea.Create(Self));
TLinea(FLineas[Result]).Indice:= Result;
end;
function TMalla.AddNodo: Integer;
begin
Result:= FNodos.Add(TNodo.Create(Self));
end;
constructor TMalla.Create(AForm: TForm);
begin
if AForm = Nil then
Raise Exception.Create('Atención: La referencia no es valida');
FZona:= AForm;
FSalida:= TNodo.Create(Self);
FDestino:= TNodo.Create(Self);
FNodos:= TList.Create;
FLineas:= TList.Create;
end;
destructor TMalla.Destroy;
begin
//limpiamos la lista de nodos
VaciarNodos;
FreeAndNil(FNodos);
//limpiamos la lista de lineas
VaciarLineas;
FreeAndNil(FLineas);
//nos desvinculamos del objeto padre
//sobre el que nos mostramos
FZona:= Nil;
FreeAndNil(FSalida);
FreeAndNil(FDestino);
inherited Destroy;
end;
procedure TMalla.DibujaRuta;
var
i: Integer;
FNodo: TNodo;
begin
VaciarLineas;
fNodo:= Nil;
for i := 0 to CountNodos - 1 do begin
if FNodo <> Nil then begin
FNodo.AddLinea(Nodos[i]);
end
else FSalida.AddLinea(Nodos[i]);
FNodo:= Nodos[i];
end;
FNodo.AddLinea(FDestino);
end;
procedure TMalla.DoDibujarMalla;
var
i: Integer;
begin
if Assigned(FZona) then begin
for i := 0 to CountLineas - 1 do Lineas[i].DibujarLinea;
for i := 0 to FNodos.Count - 1 do Nodos[i].DibujarNodo;
Salida.DibujarNodo;
Destino.DibujarNodo;
end;
end;
procedure TMalla.DoOrdenaNodos(ANodo: TNodo; AOrdenacion: TOrdenacion);
begin
AOrdenacion(Self, ANodo);
end;
function TMalla.GenerarRuta: Double;
begin
if (CountNodos = 0) or (FSalida = Nil) or (FDestino = Nil) then
Raise Exception.Create('Error: No existe suficente información en la ruta a generar');
OrdenarNodos;
DibujaRuta;
Result:= CalculaMetricaRuta;
end;
function TMalla.GetLineas(Indice: Integer): TLinea;
begin
if (Indice < 0) or (Indice > FLineas.Count-1) then
Raise Exception.Create('Error en el valor del indice de la matriz');
Result:= FLineas[Indice];
end;
function TMalla.GetNodos(Indice: Integer): TNodo;
begin
if (Indice < 0) or (Indice > FNodos.Count-1) then
Raise Exception.Create('Error en el valor del indice de la matriz');
Result:= FNodos[Indice];
end;
procedure TMalla.InicializarMalla;
begin
VaciarLineas;
VaciarNodos;
FPivote:= Nil;
end;
procedure TMalla.InternalOrdenaNodos(Sender: TObject; ANodo: TNodo);
procedure OrdenaQuickSort(L,R: Integer);
var
i,j: Integer;
piv, aux: TNodo;
begin
i:= L;
j:= R;
piv:= Nodos[(L+R) div 2]; //pivote
Repeat
while (Nodos[i].GetDistancia < piv.GetDistancia) do Inc(i);
while (piv.GetDistancia < Nodos[j].GetDistancia) do Dec(j);
if i<= j then begin
Aux:= Nodos[i];
FNodos.Exchange(i,j);
FNodos[j]:= Aux;
Inc(i);
Dec(j);
end;
if L<j then OrdenaQuickSort(L,j);
if i<R then OrdenaQuickSort(i,R);
Until i>j;
end;
begin
OrdenaQuickSort(ANodo.GetIndice, CountNodos-1);
end;
procedure TMalla.OrdenarNodos;
var
i: Integer;
begin
FPivote:= FSalida;
for i := 0 to CountNodos - 1 do
OrdenarNodos(Nodos[i], FDestino);
end;
procedure TMalla.OrdenarNodos(ANodo: TNodo; ADestino: TNodo);
var
i: Integer;
begin
//guardamos el indice del vector para que calcule la distancia
//correctamente ya que el pivote debe avancar
i:= ANodo.GetIndice;
DoOrdenaNodos(ANodo, InternalOrdenaNodos);
//en este punto el nodo puede haber cambiado
FPivote:= Nodos[i];
end;
procedure TMalla.SetSalida(const Value: TNodo);
begin
if FSalida = nil then
FSalida := Value;
end;
procedure TMalla.VaciarLineas;
var
i: Integer;
begin
for i := 0 to CountLineas - 1 do begin
TLinea(FLineas[i]).Free;
FLineas[i]:= Nil;
end;
FLineas.Clear;
end;
procedure TMalla.VaciarNodos;
var
i: Integer;
begin
for i := 0 to CountNodos - 1 do begin
TNodo(FNodos[i]).Free;
FNodos[i]:= Nil;
end;
FNodos.Clear;
end;
function TMalla.CalculaMetricaRuta: Double;
var
i: Integer;
begin
Result:= 0;
for i := 0 to CountLineas - 1 do begin
Result:= Result + TLinea(FLineas[i]).GetDistancia;
end;
end;
function TMalla.CountLineas: Integer;
begin
Result:= FLineas.Count;
end;
function TMalla.CountNodos: Integer;
begin
Result:= FNodos.Count;
end;
{TNodo}
procedure TNodo.DibujarNodo;
begin
if not Assigned(Self) then Exit;
if (Self = FMalla.Salida) or
(Self = FMalla.FDestino) then begin
if (Self = FMalla.Salida) then begin
FShape.Brush.Color:= clRed;
FShape.Pen.Color:= clRed;
end
else begin
FShape.Brush.Color:= clBlue;
FShape.Pen.Color:= clBlue;
end;
end
else begin
FShape.Brush.Color:= clLime;
FShape.Pen.Color:= clGreen;
FMalla.FZona.Canvas.Font.Size:= 7;
FMalla.FZona.Canvas.TextOut(X-12,Y-12,'('+InTToStr(GetIndice)+')')
end;
end;
function TNodo.AddLinea(ANodoTarget: TNodo): Integer;
var
fLin: TLinea;
begin
if ANodoTarget = Nil then
Raise Exception.Create('Atención: La referencia al nodo no es valida');
Result:= FMalla.AddLinea;
if Result >= 0 then
FMalla.Lineas[Result].Enlaza(Self, ANodoTarget);
end;
constructor TNodo.Create(AMalla: TMalla);
begin
if AMalla = Nil then
Raise Exception.Create('Atención: La referencia no es valida');
FMalla:= AMalla;
FShape:= TShape.Create(Nil);
FShape.Parent:= AMalla.FZona;
FShape.Shape:= stCircle;
FShape.Height:= 8;
FShape.Width:= 8;
if Self = FMalla.Salida then begin
FShape.Brush.Color:= clRed;
FShape.Pen.Color:= clRed;
end
else begin
FShape.Brush.Color:= clLime;
FShape.Pen.Color:= clGreen;
end;
FPeso:= 0;
x:= 0;
y:= 0;
end;
destructor TNodo.Destroy;
begin
FMalla:= Nil;
FreeAndNil(FShape);
inherited;
end;
function TNodo.GetDistancia: Double;
begin
Result:= CalcularDistanciaNodos(FMalla.FPivote, Self);
end;
function TNodo.GetIndice: Integer;
var
i: Integer;
begin
i:= 0;
while i < FMalla.CountNodos do begin
if FMalla.Nodos[i] = Self then begin
Result:= i;
Exit;
end;
Inc(i);
end;
Result:= -1;
end;
function TNodo.GetX: Integer;
begin
Result:= FPoint.X;
end;
procedure TNodo.SetTag(const Value: Integer);
begin
FTag := Value;
end;
procedure TNodo.SetPeso(const Value: Integer);
begin
FPeso := Value;
end;
procedure TNodo.SetX(const Value: Integer);
begin
FPoint.X := Value;
FShape.Left:= FPoint.X;
end;
function TNodo.GetY: Integer;
begin
Result:= FPoint.Y;
end;
procedure TNodo.SetY(const Value: Integer);
begin
FPoint.Y := Value;
FShape.Top:= FPoint.Y;
end;
{ TLinea }
constructor TLinea.Create(AMalla: TMalla);
begin
FMalla:= AMalla;
FAlfa:= Nil;
FOmega:= Nil;
end;
destructor TLinea.Destroy;
begin
FMalla:= Nil;
inherited;
end;
procedure TLinea.DibujarLinea;
begin
if Assigned(FMalla) then begin
FMalla.FZona.Canvas.MoveTo(FAlfa.X, FAlfa.Y);
FMalla.FZona.Canvas.LineTo(FOmega.X, FOmega.Y);
end;
end;
function TLinea.GetDistancia: Double;
begin
Result:= FDistancia;
end;
procedure TLinea.Enlaza(AAlfa, AOmega: TNodo);
begin
if AAlfa = AOmega then
Raise Exception.Create('No se pueden enlazar dos nodos iguales');
if AAlfa <> FAlfa then FAlfa:= AAlfa;
if AOmega <> FOmega then FOmega:= AOmega;
FDistancia:= CalcularDistanciaNodos(FAlfa, FOmega);
end;
procedure TLinea.SetAlfa(const Value: TNodo);
begin
if Value <> FOmega then FAlfa := Value;
FDistancia:= CalcularDistanciaNodos(FAlfa, FOmega);
end;
procedure TLinea.SetIndice(const Value: Integer);
begin
FIndice := Value;
end;
procedure TLinea.SetOmega(const Value: TNodo);
begin
if Value <> FAlfa then FOmega := Value;
FDistancia:= CalcularDistanciaNodos(FAlfa, FOmega);
end;
end.
Y esta es la imagen, una vez generada la ruta:
El asterisco (*) venía a cuento cuando comentaba que podíais modificar facilmente el ejemplo para que calculara la ruta no en función de recorrer todos los nodos sino aquellos que pudieran hacer menor la distancia. Para ello, quizás bastaría modificar el calculo de la distancia, sobrescribiendo la función virtual
DoOrdenaNodos(ANodo: TNodo; AOrdenacion: TOrdenacion); virtual;
Y entregando como parámetro una nueva función que ademas, tuviera en cuenta no solo la distancia de los dos nodos sino también el calculo con respecto al punto de destino. Y una vez obtenido ese recalculo, compararlo en cada uno de los avances del vecto con el punto final. Podría ser una idea.
Como hicimos en la entrada anterior vamos a intentar destacar algunas ideas importantes que os pueden servir de guia:
* Este es un ejemplo y no deja de serlo aunque calcule un resultado. Os comento ésto porque este resultado puede ser correcto para mi, en el dominio de una aplicación concreta y no ser para otros requerimientos, puesto que no existe realmente una optimización al generar la ruta, ni existen caminos que precondicionen optar por una ruta o por otra. Aqui hemos cogido puntos al azar y nos hemos imaginado la forma de recorrerlos todos.
* Otro punto que parece interesante y por eso lo he incluido así, es el paso de una función como parámetro, que nos permite reutilizar el metodo ante la necesidad de tener en cuenta nuevas condiciones. Para ello, nos basta sobrescribir el método, que es algo realmente sencillo. En este caso concreto, el método tiene un tipo declarado en el interfaz de la unidad UNodos.pas (TOrdenacion = procedure(Sender: TObject; ANodo:TNodo) of Object;)
* Y puede seros de curiosidad, por ejemplo el algoritmo QuickSort, que necesité modificar un tanto para que se reordenara en función de la distancia, como he explicado en lineas anteriores.
* El tratamiento de las listas de punteros (TList) y de las listas de cadenas y como podemos valernos de estas clases para almacenar y manipular referencias a objetos. Es un punto que se reitera continuamente en buena parte del código que podais encontrar, ya que son clases muy básicas.
* Y como siempre, teniendo en cuenta la reutilización. Aunque no lo he comentado, creo que incluso podríamos haber hecho uso del generador de códigos (visto en la entrada anterior), haciendo una ligera modificiación para que nos pudiera calcular distintas combinaciones de nodos y ofrecer a nuestro usuario, la posibilidad de elegir entre varias rutas alternativas.
Con un poco de imaginación quizás no hablariamos de distancia. Es una de las razones que me han hecho añadir la propiedad Peso en el Nodo, aunque luego no le he dado ninguna utilidad. ¿Una combinación de factores, distancia y peso y otros que pudieramos considerar? ¡Hay tantas posibilidades que en nuestro pequeño ejemplo nos hemos intentado quedar con la más didáctica y no enrevesar el código con mayor complejidad que no nos iba a aporatar realmente nada.
Yo creo que podemos dejarlo en este punto. La idea era compartir con vosotros las ventajas de razonar en términos de clases, de intentar en la medida que nos sea posible abstraernos y hacer que nuestro código sea lo mas reutilizable posible. Si bien es cierto que a corto plazo puede ser un inconveniente porque implica un mayor esfuerzo, a largo plazo es rentable, tanto a nivel de reusabilidad como de adaptabilidad a nuevos requerimientos.
Espero que os puedan ayudar estas lineas.

Muy inteesante (como siempre, por otra parte) la entrada Salvador.
Además de las explicaciones, el código resulta muy claro.
Esta entrada es de las que interesa conservar, porque antes o después llega este problema (o relacionado). Hace unos meses, salió en mi empresa un tema relacionado con el cálculo de rutas para repartos (camioneros); Estoy seguro que antes o depués volverá a salir… ;-D
Un saludo.
Me gustaMe gusta
Gracias Germán.
🙂
Me alegra que se pueda encontrar interesante lo que voy añadiendo al blog. Todos aportamos nuestro granito de arena a esta comunidad.
Un saludo,
Salvador
Me gustaMe gusta